Premetto che i commenti sono puramente scientifici, non sono un esperto di diritto. La sentenza tuttavia si dilunga in una serie di interpretazioni di dati e di pubblicazioni scientifiche, arrivando a delle conclusioni errate. A pag.57 della sentenza, §2.3, si legge:
La rappresentazione grafica appena effettuata consente di apprezzare in modo intuitivo ed immediato l’andamento del numero di scosse registrate nel corso dei mesi.
Appare evidente in proposito che, a partire da gennaio 2009, il distretto
aquilano ha registrato una chiara impennata di valori. I grafici sopra disegnati rappresentano con evidente forza icastica come, nel periodo 1.1.09 – 31.3.09, nei tre distretti Monti della Laga, Monti Reatini e Gran Sasso vi sia stato un decremento del numero di scosse rispetto ai sei mesi precedenti, mentre nel distretto Aquilano vi è stata una crescita marcata che raggiungeva il suo acme nel mese di marzo 2009.
Si tratta di una parte di un commento abbastanza lungo (pagg.55-66) sull'analisi delle frequenza di scosse a bassa intensita' ("precursori") che flagellavano l'Abruzzo a partire dal giugno 2008. Il giudice si dilunga in una discussione, il cui senso sintetizzando e’: erano presenti dei precursori (sciame sismico a intensita’ bassa), chiamiamo evento A, che ha preceduto l’evento B (terremoto distruttivo del 6 aprile 2009). La scienza e’ tutta basata su correlazioni, tuttavia la correlazione deve essere significativa (diciamo, >50%), poi deve esserci una connessione di causalita’. Il fatto che nella sentenza stessa si dica che la correlazione si perde quando si considera una regione piu’ ampia (il brano citato, piu' il grafico a Pag.56 confrontato col grafico a Pag.57) depone male, nel senso che, quando una correlazione diminuisce considerando un campione statistico con un numero maggiore di eventi, questo fatto e’ piu’ un indizio di risultato spurio dovuto a campione insufficiente, che non l’insight di chissa’ quale meccanismo nascosto. Anche ammettendo di avere una statistica sufficiente, un’alta correlazione di eventi A che precedono eventi B, non garantisce che A generi B: potrebbe esserci un terzo evento C che causa entrambi i fenomeni A e B. L’eventualita’ di una presenza di un confounding factor C aumenta grandemente quando la correlazione non e’ significativa, come evidenzia bene un recente lavoro sugli ecosistemi marini (Sugihara & May, 2012).
Forse a sostegno della teoria del “precursore” del §2.3, e della sua lettura biased della testimonianza di Selvaggi a pag.58, il giudice aggiunge una disamina della pubblicazione (Boschi, Gasperini, & Mulargia, 1995): a pag.278 della sentenza si legge,
Forse a sostegno della teoria del “precursore” del §2.3, e della sua lettura biased della testimonianza di Selvaggi a pag.58, il giudice aggiunge una disamina della pubblicazione (Boschi, Gasperini, & Mulargia, 1995): a pag.278 della sentenza si legge,
Sempre sul tema della pericolosità sismica del territorio aquilano e delle
previsioni probabilistiche di forti terremoti, il prof. BOSCHI nel 1995
pubblicava sulla rivista internazionale "Bulletin of the seismological society of America” (vol. 85, n. 5, pp. 1475 – 1482) un articolo dal titolo “L’individuazione preventiva dei luoghi in cui potrebbero verificarsi gravi terremoti nell’immediato futuro” [...]
La tabella 4 evidenzia che:
“la regione 34 (Aquilano) ha un P pari a 1 di probabilità di occorrenza di un terremoto con di magnitudo pari o maggiore a 5.9 nei prossimi 5, 20, 100 anni utilizzando sia il processo di Gauss che quello di Poisson per l’occorrenza degli eventi secondo il coefficiente di variazione” (tabella 4, pag. 6).
Sostenere che il coefficiente probabilistico (P) è pari a 1 (“di fatto uguale
all’unità”) significa affermare che il grado di probabilità non è soltanto molto elevato, ma è addirittura prossimo alla certezza (certezza = 1).
Il giudice ritiene una prova a favore della sua tesi sul "precursore” il fatto che il tempo di attesa per l’Aquilano di un terremoto M>5.9 sia di circa 61 anni, e che uno degli intervalli in cui la pubblicazione (Boschi, Gasperini, & Mulargia, 1995) considera la valutazione della probabilita’ termina nel 2015. Innanzitutto, come evidenzia bene il prof.Zanella dell'Universita' di Padova, la valutazione del tempo di attesa di un terremoto nell'aquilano (prima del 2009) era basata su soli 3 eventi, e il tempo trascorso da quegli eventi era almeno 4 volte il tempo di attesa, rendendo praticamente irrilevante l'osservazione che P=1 nel distretto 34 (Aquilano). Lo stesso Boschi annota nella sua pubblicazione del 1995
Note that the high probability of region 34 comes from the fact that after
three almost exactly spaced earthquakes (61 + 2 yr) no large
magnitude activity occurred in the following 200 yr.
In ogni caso, anche prendendo per buona la valutazione del tempo di attesa di 61 anni, il tempo di attesa (waiting time) e’ un tipico concetto stocastico, che ha senso in termini di distribuzione: in particolare, con qualsiasi distribuzione di probabilita’, la probabilita’ di un evento in un intervallo infinitesimo di tempo e’ nulla. Il tempo di attesa non e’ una sveglia, che suona allo scoccare del 2015 e, soprattutto, il punto del giudice e’ una valutazione della probabilita’ nel periodo in cui i cosiddetti “precursori” avvengono, quindi a distanza di 1 anno. Supponiamo che i terremoti siano degli eventi scorrelati, per i quali vale un processo di Poisson con distribuzione esponenziale dei tempi di attesa :
Il significato e' che la funzione a membro di destra esprime la probabilita' che l'evento X si ripeta k volte nell'intervallo (0,t]. Un concetto fondamentale e' che la probabilita' di Poisson e' indipendente da t, quindi P(t,t+t1)=P(0,t1). Calcolare la probabilita' nel 2005 o nel 1762 e' la stessa cosa.
Dice inoltre un'altra cosa: calcolare la probabilita', che so, dal 2013 al 2014, adesso che c'e' stato un evento distruttivo nel 2009, e' la stessa che dal 2008 al 2009 (anche se ovviamente il tempo di attesa tau va ricalcolato, essendo una statistica bassa). Dire il contrario significherebbe che c'e' una correlazione (anti-correlazione, per esempio) tra gli eventi, cosa che contraddice l'uso di un processo di Poisson. A quanto la scienza ne sa, prove di correlazione fra terremoti ("clustering") sono ancora deboli. L'articolo di Boschi (1995) voleva appunto tentare di dirimere una questione di questo tipo, ma evidentemente il giudice ha completamente travisato il messaggio.
L'esponenziale exp(-t/tau) esprime il fatto che la probabilita' dell'evento e' molto piccola su tempi piu' piccoli di tau, che e' il tempo di attesa (medio). Esprime quanto abbiamo detto sopra, la probabilita' di un evento in un intervallo infinitesimo e' zero.
Un caso particolare della distribuzione e' quando k=0: la probabilita' che un evento non si verifichi. In quel caso, prendendo per buona la valutazione del tempo di ritorno tau=61 anni, e pensando di trovarsi in un intervallo largo t=1 anno:
Dice inoltre un'altra cosa: calcolare la probabilita', che so, dal 2013 al 2014, adesso che c'e' stato un evento distruttivo nel 2009, e' la stessa che dal 2008 al 2009 (anche se ovviamente il tempo di attesa tau va ricalcolato, essendo una statistica bassa). Dire il contrario significherebbe che c'e' una correlazione (anti-correlazione, per esempio) tra gli eventi, cosa che contraddice l'uso di un processo di Poisson. A quanto la scienza ne sa, prove di correlazione fra terremoti ("clustering") sono ancora deboli. L'articolo di Boschi (1995) voleva appunto tentare di dirimere una questione di questo tipo, ma evidentemente il giudice ha completamente travisato il messaggio.
L'esponenziale exp(-t/tau) esprime il fatto che la probabilita' dell'evento e' molto piccola su tempi piu' piccoli di tau, che e' il tempo di attesa (medio). Esprime quanto abbiamo detto sopra, la probabilita' di un evento in un intervallo infinitesimo e' zero.
Un caso particolare della distribuzione e' quando k=0: la probabilita' che un evento non si verifichi. In quel caso, prendendo per buona la valutazione del tempo di ritorno tau=61 anni, e pensando di trovarsi in un intervallo largo t=1 anno:
Quindi, la probabilita' che l'evento si verifichi e' 1-0.984=0.016. E' una probabilita' molto piccola, intorno all'1%: la probabilita’ a un anno rimane piccola, anche se la probabilita’ cumulativa puo’ essere alta. La probabilita' mensile o settimanale e' 1/12 di questa, quindi dell'ordine 1/1000, oppure 0.1%. E’ l’errore di chi scommette al lotto sui numeri “mancanti” da molto tempo, pensando che la probabilita’ di vincere in questo modo cresca.
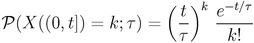
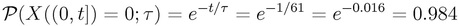
 RSS Feed
RSS Feed



