Giusto per fare un esempio, ci si puo' scaricare il file (excel o testo) dei terremoti storici nella regione de L'Aquila, al sito http://emidius.mi.ingv.it/DBMI11/query_place/
Selezionando i terremoti con M>5.9, si raggruppano gli eventi per t>1400 yr, con dei bin di lunghezza opportuna: l'analisi dipende un po' dalla scelta della lunghezza del bin, diciamo che si puo' optare fra 20 e 50 anni.
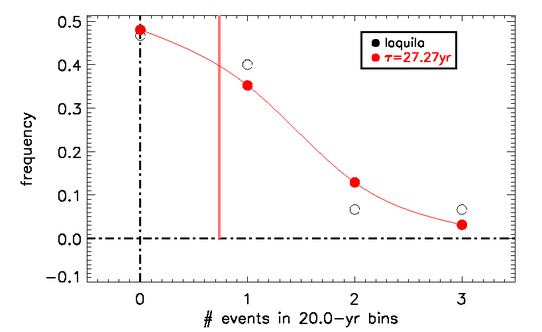
Si contano gli eventi nei singoli bin, per es. nell'intervallo [1400,1420], [1420,1440], [1440,1460], e cosi' via. Si fa una statistica del numero di intervalli che totalizzano un determinato numero k di eventi: numero di bins con k=0 eventi, numero di bins con k=1 eventi, e cosi' via. Dividendo il numero di bins, N(k), per il numero totale di bins, cioe' la somma di N(k) su tutti i k, si ottiene la stima della probabilita' p(k). Il risultato sono i pallini vuoti neri del grafico qui sotto:
Selezionando i terremoti con M>5.9, si raggruppano gli eventi per t>1400 yr, con dei bin di lunghezza opportuna: l'analisi dipende un po' dalla scelta della lunghezza del bin, diciamo che si puo' optare fra 20 e 50 anni.
Si contano gli eventi nei singoli bin, per es. nell'intervallo [1400,1420], [1420,1440], [1440,1460], e cosi' via. Si fa una statistica del numero di intervalli che totalizzano un determinato numero k di eventi: numero di bins con k=0 eventi, numero di bins con k=1 eventi, e cosi' via. Dividendo il numero di bins, N(k), per il numero totale di bins, cioe' la somma di N(k) su tutti i k, si ottiene la stima della probabilita' p(k). Il risultato sono i pallini vuoti neri del grafico qui sotto:
Ora possiamo calcolare la media, data da
e, nota la media (linea verticale rosso chiaro), calcolare la distribuzione di Poisson (in rosso) e il tempo di attesa, che risulta essere di 27,27 anni. La curva di Poisson mi dice che, nell'arco temporale del mio bin (20 anni), ho la probabilita' exp(-20/27)=0.48 di non avere mai un terremoto, 20/27*exp(-20/27)=0.35 di averne uno, 0.5*(20/27)^2 * exp(-20/27)=0.13 di averne due.
Qui si capisce anche la fallacia del ragionamento del giudice Billi: se considero un intervallo di tempo spropositatamente lungo, per esempio, duecento anni, la probabilita' di non avere un terremoto, cioe' la probabilita' di Poisson P(k=0,mu), crolla ad essere exp(-200/27)=0.0006. Cioe' anche, la probabilita' di avere un terremoto e' 1-0.0006, praticamente uno, certezza.
Beh, caro giudice Billi, se uno ha la fortuna di vivere 200 anni a L'Aquila, e' chiaro che avra' la certezza di vedere un altro terremoto M>5.9
Nell'attesa che Matuselemme oppure Noe' dessero una risposta, agli scienziati il 31 marzo 2009 fu chiesto se, nei limiti della conoscenza e delle leggi della statistica, a breve ci sarebbe stato o no un terremoto (a causa dei cosiddetti "precursori"). E non di li' a 200 anni!!!
Sembra che il giudice Billi e il PM Picuti abbiano un concetto abbastanza peculiare di probabilità e certezza: per parafrasare un pezzo di spirito del fisico Robert Park, autore del memorabile libro Voodoo Science, se mi dicono che un brontosauro sta attraversando Broadway, beh, sì, è possibile, forse anche certo, ammesso che io abbia vissuto 95 milioni di anni. Ma, dato che la vita media di un uomo è di 70-80 anni (quando va bene), è più probabile che io abbia visto un cavallo e lo abbia scambiato per un brontosauro.
Qui si capisce anche la fallacia del ragionamento del giudice Billi: se considero un intervallo di tempo spropositatamente lungo, per esempio, duecento anni, la probabilita' di non avere un terremoto, cioe' la probabilita' di Poisson P(k=0,mu), crolla ad essere exp(-200/27)=0.0006. Cioe' anche, la probabilita' di avere un terremoto e' 1-0.0006, praticamente uno, certezza.
Beh, caro giudice Billi, se uno ha la fortuna di vivere 200 anni a L'Aquila, e' chiaro che avra' la certezza di vedere un altro terremoto M>5.9
Nell'attesa che Matuselemme oppure Noe' dessero una risposta, agli scienziati il 31 marzo 2009 fu chiesto se, nei limiti della conoscenza e delle leggi della statistica, a breve ci sarebbe stato o no un terremoto (a causa dei cosiddetti "precursori"). E non di li' a 200 anni!!!
Sembra che il giudice Billi e il PM Picuti abbiano un concetto abbastanza peculiare di probabilità e certezza: per parafrasare un pezzo di spirito del fisico Robert Park, autore del memorabile libro Voodoo Science, se mi dicono che un brontosauro sta attraversando Broadway, beh, sì, è possibile, forse anche certo, ammesso che io abbia vissuto 95 milioni di anni. Ma, dato che la vita media di un uomo è di 70-80 anni (quando va bene), è più probabile che io abbia visto un cavallo e lo abbia scambiato per un brontosauro.
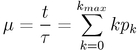
 RSS Feed
RSS Feed



