di Owen Gingerich (Professore emerito, dipartimento di Astrofisica, Harvard-Smithsonian Center for Astrophysics, Cambridge, Massachussets)
Nell'agosto 1593 Tycho Brahe era in forte preoccupazione, una doppia preoccupazione. Era appena ritornato alla sua isola-osservatorio di Hven da un viaggio inutile alla corte di Copenhagen. Si vantava del fatto che Federico II, il defunto re di Danimarca e Norvegia, avesse speso una tonnellata d'oro per costruire l'osservatorio di Uraniburg sull'isola di Hven, l'osservatorio piu' avanzato di allora in Europa, ma Tycho non aveva idea di quale sarebbe stato l'atteggiamento del successore di Federico. Peggio ancora, Tycho, un nobile, si era unito a una donna non nobile, una sorta di Kate Middleton dell'epoca. Secondo la legge danese, la moglie non nobile e i suoi figli non avrebbero mai potuto ereditare il prezioso osservatorio di Uraniburg. Che ne sarebbe stato di quel gioiello di tecnologia?
Nel frattempo, aveva anche forti preoccupazioni per i suoi dati sull'orbita di Marte. E come si sarebbe evidenziato nelle settimane successive, il problema era anche peggiore di quello che Tycho potesse immaginare.
Andiamo indietro di dieci anni: Tycho escogita un metodo ingegnoso per distinguere la cosmologia tolemaica e copernicana, il grande cruccio della scienza dell'epoca. Entrambi i sistemi prevedono essenzialmente le stesse posizioni planetarie. Ma nel sistema tolemaico Marte gira su un'orbita al di la' di quella del Sole, e pertanto la sua distanza minima dalla Terra e' di una unita' astronomica (AU). Nel sistema copernicano Marte e' oltre l'orbita terrestre, per cui la distanza minima e' di sole 0.5 AU, meta' di quella nel sistema Tolemaico. Se Tycho avesse potuto misurare questa distanza, questo sarebbe stato una prova determinante, un experimentum crucis per distinguere le due cosmologie.
Tycho propose di usare il metodo noto come parallasse diurna: la misura si doveva effettuare quando Marte fosse all'opposizione, nel qual caso necessariamente sarebbe stato piu' vicino alla Terra. A quel punto Tycho avrebbe misurato la posizione di Marte subito dopo il tramonto, con Marte che appena sorgeva a Est. Avrebbe poi ripetuto la misura poco prima del sorgere del Sole, con Marte che tramontava a Ovest. Se avesse effettuato questa misura all'Equatore, la rotazione della Terra avrebbe fornito una base di triangolazione uguale al diametro terrestre. A una latitudine piu' settentrionale, la base sarebbe stata un po' piu' corta, ma ancora lunga abbastanza per lo scopo.
Oggi sappiamo che questa misura e' impossibile con osservazioni a occhio nudo, come quelle che faceva Tycho Brahe. Ma nel sedicesimo secolo tutti accettavano una valutazione erronea della distanza fra Terra e Sole, una valore di circa 20 volte minore di quello reale. Se questo valore fosse stato vero, le misure di Tycho (incredibilmente precise per l'epoca) avrebbero fornito il risultato desiderato. Ma non sapendolo, Tycho cadde in errore.
Le tavole di rifrazione
Marte e' all'opposizione (cioe', dalla parte opposta al Sole rispetto alla Terra) mediamente ogni 2 anni e 7 settimane. Tycho tento' di trovare la distanza di Marte col suo ingegnoso metodo nel dicembre 1582, ma senza successo; i suoi strumenti non erano ancora abbastanza accurati. Armato di ulteriori migliorie al suo osservatorio, e con strumenti piu' stabili, tento' di nuovo nel gennaio 1585. Ma con grande sorpresa (e non poco fastidio) ottenne una parallasse negativa, il che implicava che Marte fosse piu' che infinitamente lontano. Capi' subito che questo risultato era assurdo, e intui' il problema: quella che noi chiamiamo adesso rifrazione differenziale. Normalmente Tycho misurava la parallasse per oggetti ben alti nel cielo, ma la sua procedura della parallasse diurna richiedeva di osservare Marte quando era poco lontano dall'orizzonte, dove la rifrazione atmosferica solleva stelle e pianeti di poco al di sopra della loro posizione reale. Poiche' le stelle su cui Tycho si calibrava erano ad altezze diverse da Marte, bisognava correggere per la rifrazione atmosferica.
Percio' Tycho decise di compilare una tabella di rifrazioni, anzi,due per la precisione. Per determinare la quantita' di rifrazione si deve conoscere l'altezza vera di un oggetto. Tycho aveva due metodi per calcolare questa altezza vera: una col Sole, e una con le stelle. Nel caso del sole, ricavo' una teoria del moto solare per ricavare la posizione vera del sole, da confrontare con l'altezza a mezzogiorno ottenuta tramite una grande meridiana su uno dei muri interni del suo castello. Tuttavia, nella sua teoria del moto solare, Tycho uso' ancora la stima errata della distanza Terra-Sole, col risultato di valutare in modo scorretto l'eccentricita' dell'orbita solare. In conseguenza, anche la tabella di rifrazioni dedotta dal sole era leggermente sbagliata.
Per le stelle, Tycho uso' il suo strumento piu' impressionante, la sfera armillare equatoriale, il cui diametro era di 2.7m. Con questo strumento, Tycho poteva misurare direttamente nello stesso momento la declinazione e l'altezza di una stella (cioe', la distanza angolare dall'equatore e dall'orizzonte, rispettivamente). La rifrazione modifica la declinazione della stella, che altrimenti dovrebbe rimanere costante: misurando la variazione in declinazione mentre la stella saliva e scendeva in altezza, pote' compilare una seconda tabella di rifrazioni.
Nel marzo 1587 Marte era di nuovo all'opposizione, e Tycho si lancio' in una nuova campagna di osservazioni. Ma quale tabella di rifrazioni usare, quella solare o quella stellare? Dopo avere applicato la tabella solare, ottenne dei valori di parallasse vicini a quelli previsti dalla teoria Copernicana, rendendosi poco conto che i valori ottenuti erano un artefatto della tabella di rifrazioni sbagliata.
Per ironia della sorte pero', Tycho non era un copernicano convinto: benche' matematicamente la teoria di Copernico filasse liscia, egli non era convinto che dinamicamente un oggetto massiccio come la Terra potesse muoversi vorticosamente intorno al Sole. Opto' quindi per una soluzione ibrida, geo-eliocentrica. Nel sistema detto "Ticonico", la Terra era ancora immobile al centro dell'Universo, mentre Marte girava intorno al Sole, e a sua volta il Sole girava intorno alla Terra [per inciso, questa soluzione fece imbufalire Galileo, il quale la bolla senza mezzi termini nel "Dialogo dei Massimi Sistemi"]. La distanza minima Terra-Sole nel sistema ticonico e copernicano e' la stessa, meta' del caso tolemaico.
Tuttavia, Tycho era uno scienziato brillante, e non era certamente il tipo che si lasciasse abbagliare da una scelta arbitraria della tabella di rifrazione. Volle testare il suo risultato, e lo fece sul pianeta Giove. Scopri' il suo errore, e quindi passo' sotto silenzio le sue misure della distanza Terra-Marte.
Dopo marzo 1587, la successiva tornata di opposizioni coincideva con le ben corte notti estive del giugno 1591. Ma Tycho fu di nuovo sul campo nell'agosto 1593. Ma, dopo il suo orribile ritorno da Copenhagen, pure il tempo era orribile: vento, pioggia, temporali sono riportati sul suo diario di osservazioni. Alla fine, il 13 agosto i cieli si riaprirono, e Tycho tabulo' i suoi risultati sul suo diario:
Declinazione Deviazione osservata
Tavole pruteniche 342°0' -4°7.50'
(Copernicane)
Osservazioni Tycho 346°7.50' ==
Tavole Alfonsine 351°26' +5°18.5'
(Tolemaiche)
Fu uno shock catastrofico: il pianeta rosso non era neppure lontanamente vicino alle previsioni, in una qualunque delle due cosmologie. I valori erano errati di 4 o 5 gradi, ben al di la' dell'incertezza sperimentale degli apparati sofisticati di Tycho, in direzioni opposte, e rimasero tali per molte settimane. [per valutare l'errore, tenete conto che il diametro apparente in cielo della luna o del sole e' di mezzo grado!].
Nel novembre 1600 Tycho rusci' a risolvere il problema ereditario: parti' infatti dalla Danimarca diretto alla corte dell'imperatore Rodolfo II, portandosi dietro famiglia e strumenti astronomici. A Praga le leggi erano diverse, li' la moglie e figli avrebbero ereditato i suoi beni. Circa un anno dopo il suo arrivo, Tycho aggiunse un nuovo, giovane assistente al suo staff: Giovanni Keplero, un insegnante di scuola superiore di religione luterana, che improvvisamente si era ritrovato senza lavoro a causa dell'ondata di Controriforma cattolica che aveva investito il sud della Germania, Austria e Boemia comprese. Alle dipendenze di Tycho Brahe, Keplero si occupo' del problema di Marte. Rimane un mistero se mai Tycho comunico' a Keplero della "catastrofe" di Marte dell'agosto 1593. Forse, ma nessuno lo sa di sicuro. In ogni caso, Keplero lo avrebbe di sicuro scoperto nei diari di Tycho.
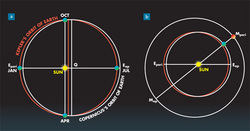
Keplero subito capi' che il problema non stava in Marte, ma nell'orbita assegnata alla Terra. Contrariamente all'opinione che oggi e' molto diffusa ma anche errata, il sistema proposto da Copernico implicava che i pianeti non girassero su orbite circolari centrate sul Sole,ma su orbite eccentriche, e che ruotassero piu' veloci quando piu' vicini al Sole [vedi figura sopra]. La Terra era l'unica eccezione, in quanto si pensava che avesse un'orbita eccentrica, ma che si muovesse ugualmente di moto uniforme. E Keplero dedusse che questo fatto dovesse per forza essere sbagliato.
Nell'antico universo geocentrico, i cieli giravano continuamente di moto vorticoso intorno alla Terra, una rotazione completa al giorno. Le stelle fisse si muovevano piu' veloci di tutti, e i pianeti un po' piu' lenti, fino alla Luna, che arrancava lentamente dietro a tutti. La sorgente della rotazione era, secondo l'insegnamento di Aristotele, la bonta' di Dio, che dava origine al moto al di la' del firmamento (motore immobile).
Nel sistema Copernicano, al contrario, le stelle erano un sistema di riferimento esterno e fisso. Pertanto, l'energia che dava moto al sistema planetario doveva provenire dall'interno, dal Sole stesso. E cio' aveva senso per Copernico, che aveva notato che quanto piu' vicino un pianeta era al Sole, tanto piu' veloce si muoveva. Infatti, questa disposizione estetica era la motivazione prima che spinse il pionere polacco a cambiare sistema di riferimento, optando per un sistema eliocentrico. Come egli scrisse nel De Revolutionibus Orbium Coelestium, "in nessun altro modo troviamo un legame saldo di armonia fra la grandezza e il movimento delle orbite dei pianeti".
Pero' allora, perche' nel sistema copernicano la Terra era unica nell'avere una velocita' orbitale costante? Si trattava in realta' di un artefatto nella trasformazione dalla geometria geocentrica tolemaica, basata sugli epicicli e deferenti, in un sistema eliocentrico. Nel sistema copernicano, in prima approssimazione, la posizione osservata di un pianeta e' determinata dalla combinazione di due cerchi, l'orbita eliocentrica della Terra e l'orbita eliocentrica del pianeta. Allo stesso modo, nel sistema Tolemaico la posizione di un pianeta e' determinata da due cerchi, il deferente, o circolo principale, e l'epiciclo. Per i pianeti superiori (Marte, Giove e Saturno) l'epiciclo giocava il ruolo dell'orbita terrestre nel sistema Copernicano; e per semplicita' Tolomeo ipotizzo' un moto uniforme nell'epiciclo, un'ipotesi che sembro' generalmente accettabile. Cosi', quando Copernico effettuo' la trasformazione, l'orbita della Terra, come gli epicicli di Tolomeo, guido' il pianeta in un moto circolare uniforme.
Al tempo di Keplero, quasi tutti gli astronomi si rivolgevano alla madre geometria per ispirarsi. Keplero era unico nel cercare delle cause fisiche per i moti celesti. Persino il suo maestro, Michael Maestlin, lo spinse a dimenticarsi delle cause fisiche e di studiare la sola geometria per trovare una spiegazione. Ma nella visione di Keplero, la velocita' costante della Terra nel sistema Copernicano non aveva alcun senso fisico. Sicuramente doveva muoversi piu' velocemente in gennaio, quando era piu' vicina al Sole. Sia nel sistema tolemaico, sia in quello copernicano, il movimento apparente del Sole era piu' veloce in gennaio per la posizione eccentrica della sua orbita (di quella della Terra nel sistema copernicano). Keplero chiamo' questo "effetto ottico". Ma Keplero voleva anche che il moto apparente complessivo fosse la somma di un effetto ottico e di un effetto fisico. Se entrambi gli effetti fossero stati di grandezza simile, allora l'eccentricita' geometrica dell'orbita terrestre avrebbe dovuto essere dimezzata. In questo caso, la distanza variabile del Sole dalla Terra sarebbe stata la meta' di quanto ipotizzato precedentemente [vedi curve rosse in figura (a)].
Ma come era possibile misurare questa differenza minima fra la distanza Terra-Sole in gennaio e in luglio? Un modo era di misurare il diametro apparente del sole nelle varie stagioni. Keplero ideo' uno strumento per misurare questo diametro, ma i risultati non erano convincenti come egli avrebbe sperato. Un secolo dopo, l'astronomo Giovanni Domenico Cassini uso' la meridiana a proiezione nella cattedrale di Bologna per dimostrare chiaramente questo effetto, guadagnandosi cosi' una grande reputazione in tutta Europa.
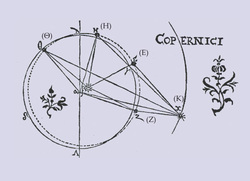
Nel frattempo, Keplero si rivolse alle misure estremamente precise che Tycho aveva fatto nelle campagne di osservazione di Marte. Un celebre diagramma nell'Astronomia nova del 1609 mostra il suo ingegnoso sistema di triangolazione. Marte ha un periodo orbitale di 687 giorni, ma ogni volta che Marte ritorna in una data posizione della sua orbita, alla Terra mancano 43 giorni per completare 2 rivoluzioni. Un osservatore dalla Terra vede pertanto Marte nella stessa posizione da due punti diversi della sua orbita. Scavando nella montagna di osservazioni accuratamente riportate da Tycho, il sistema di triangolazione di Keplero disegno' punto per punto la precisa traiettoria della Terra. Come sospettava, Keplero scopri' che l'eccentricita' dell'orbita terrestre nel sistema copernicano andava dimezzata.
Quando poi Keplero deducesse che questa modifica risolveva completamente il problema dell'orbita di Marte, non e' chiaro. Ma il passo successivo fu risolvere un problema ben piu' nascosto. Nel descrivere le posizioni eliocentriche di Marte, Keplero scopri' che l'uso di un'orbita circolare portava a un errore di 8 primi d'arco nella posizione del pianeta. Poiche' Dio aveva dispensato una cosi' grande grazia in un osservatore eccezionale come Tycho Brahe (le cui osservazioni erano affette da un errore minore o uguale a 2 primi d'arco), Keplero scrisse che non era possibile, e che non avrebbe mai accettato un errore di 8 primi. Questo errore diventava addirittura di mezzo grado quando la Terra e Marte erano piu' vicini, all'opposizione del pianeta rosso. Pertanto Keplero continuo' la sua lotta con Marte, giungendo alla fine alla celebre deduzione delle sue orbite ellittiche, che ridussero l'errore di un ordine di grandezza.
In fatti, per eliminare l'errore degli 8 primi, Keplero tento' una serie di possibili figure geometriche ovali, tutte egualmente buone all'ellisse. Ma egli era insoddisfatto dall'inconsistenza della base fisica per scegliere una qualunque di queste curve, fino a che si accorse che il fuoco di un'ellisse coincideva col Sole. Quel tipo di curva (l'ellisse) e il fuoco diedero finalmente a Keplero la giustificazione fisica che cercava. L'amico-collega di un tempo di Keplero, David Fabricius, scrisse che un fascio di cerchi avrebbe funzionato in modo eguale all'ellisse. La risposta petulante di Keplero fu: Tu dici che una figlia ti e' nata da madre geometria. L'ho vista, ed e' bellissima. Ma sara' la piu' maliziosa delle prostitute, e sedurra' i mariti dalle mie molte figlie, nate da madre fisica.
Keplero alla fine si rifiuto' di includere il modello di Fabricius nella sua Astronomia nova, e tronco' la corrispondenza con Fabricius, che durava da moltissimo tempo. Per Keplero, un modello fisico era di fondamentale importanza per fornire una spiegazione soddisfacente. Egli diede come sottotitolo alla sua opera quello di Aitiologitos, seu physica coelestis ("Eziologia, ricerca delle cause, ossia fisica celeste"). La sua lotta con Marte era finita, ma il suo libro pionieristico non sarebbe stato pubblicato se non quattro anni dopo, a causa di ritardi dovuti a schermaglie con gli eredi di Tycho, che temevano che Keplero ricavasse la crema dalle osservazioni di Tycho, riducendo quindi a nulla l'importanza della loro eredita'.
 RSS Feed
RSS Feed
